- derived from 《概率论与数理统计》 高祖新、陈华均
目录
随机事件及其运算
随机试验和随机事件
所谓随机试验是指具有以下三个特点的试验:
-
试验可在相同的条件下重复进行;
-
试验的所有结果事先是明确可知的,且不止一个;
-
每次试验恰好出现可能结果中的一个,但试验前无法预知到底出现那一结果。
我们将随机试验简称为试验。
在试验中,每个可能的结果成为基本事件,又称样本点,记为\({\omega}_0\),基本事件的全体,即实验中所有可能的结果组成的集合为试验的样本空间,记为\(\Omega\)。
由单个或多个事件组成的集合成为随机事件,简称事件,通常用大写字母\(A B C\)表示。
一个随机事件对应一个样本空间的一个子集。在随机试验中,若发生的结果是事件\(A\)包含的事件\(\omega\)就称事件\(A\)发生,记为\(\omega \in A\)。
必然事件:每次试验必然发生。不可能事件:每次试验都不会发生。
事件间的关系和运算
下面的讨论总认为是在给定的样本空间\(\Omega\)上进行,其中,\(A B C\)等是\(\Omega\)上的事件。
-
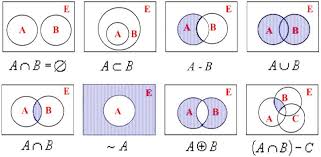
B包含A: 若A的发生必定导致B的发生,则称B包含A,记为 \(B \supset A\) 或 \(A \subset B\)。
-
A等于B: 若\(B \supset A\) 或 \(A \supset B\)。则称事件A与事件B相等,记为\(A = B\)。
-
A与B的并: 事件A与事件B中至少有一个发生所组成的事件称为事件A与B的并,记为\(A \cup B\)。
-
A与B的交: 事件A与事件B同时发生所组成的事件称为事件A与B的交,记为\(A \cap B\)。
-
A与B的差: 事件A发生而事件B不发生所组成的事件称为事件A与B的差,记为\(A - B\)。
-
A的对立事件: 对事件A,所有不属于事件A的基本事件所组成的事件称为事件A的对立事件。记为\(\overline{A}\),即\(\Omega - A\)。
-
A与B互不相容: 若A和B不能同时发生,则称A和B是互不相容,即\(A \cap B = \phi\)。
我们用下图直观地表示事件间的关系和运算。矩形表示样本空间E,圆表示事件。(图片来源:http://liyuans.net/侵删。
事件的运算满足以下规则:
- 交换律: \(A \cup B = B \cup A; A \cap B = B \cap A;\)
- 结合律: \((A \cup B) \cup C = A \cup (B \cup C); (A \cap B) \cap C = A \cap (B \cap C);\)
- 分配律: \(A \cup (B \cap C) = (A \cup B) \cap (A \cup C); A \cap (B \cup C) = (A \cap B) \cup (A \cap C);\)
- De Morgen律(对偶): \(\overline{A \cup B} = \overline{A} \cap \overline{B}; \overline{A \cap B} = \overline{A} \cup \overline{B};\)
BINISM
/
/ - views
Published under(CC) BY-NC-SA 3.0 CN.