-
禁止转载
-
derived from Prof.Huang’s slides
目录
非形式化描述
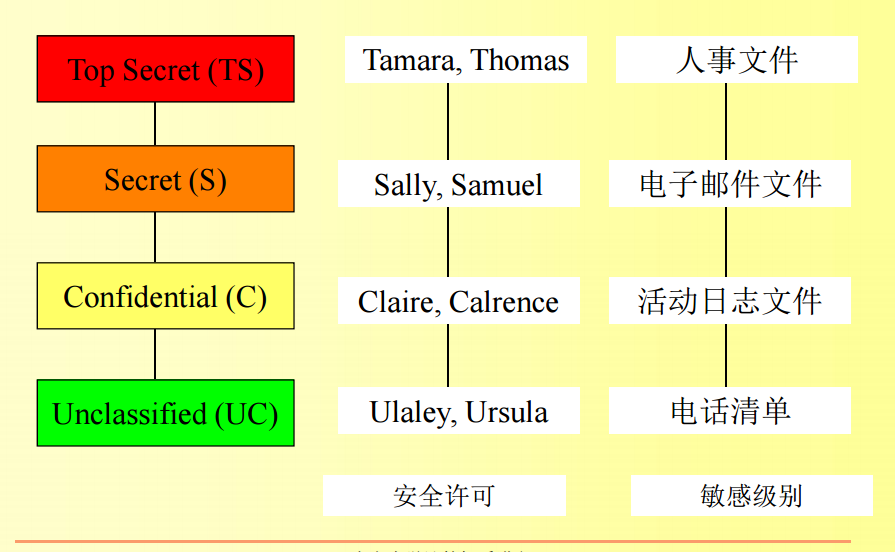
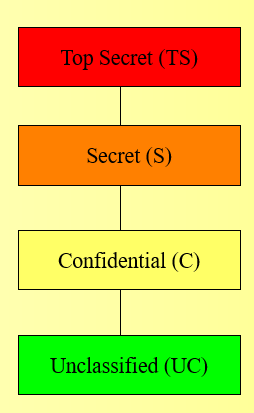
- 最简单的保密性分类形式是按照线性(全)排列的安全等级。
- 每一个主体都有一个安全许可(Clearance)。在下图中,Claire的安全许可是C(保密),Thomas的安全许可是TS(顶级机密)。
- 每个客体都有一个敏感等级,电子邮件文件的敏感等级是S(秘密),电话清单文件的敏感等级为UC(公开)。
- 当我们同时指主体的许可和客体的密级时,用术语“密级”。Bell-Lapadula安全模型的目的是要防止主体读取安全密级比它的安全许可更高的客体。
强制访问控制与自主访问控制
- 自主访问控制
- 资源的拥有者(创建者)作出决定有哪些主体可以访问这个资源。
- 由访问控制矩阵表示。
- 强制访问控制
- 由系统管理员统一制定的策略。
例如:s对o有自主的读(写)访问权
- 表示与自主访问控制部分相对应的s和o的访问控制矩阵条目中包含一项读(写)的权限。
- 如果没有强制型控制,s就可以读(写)o。
Bell—LaPadula安全模型中结合了强制型访问控制和自主型访问控制。
简单安全条件
设\(L(s)=l_s\)是主体s的安全许可,并设\(L(o)= l_o\)是客体o的敏感等级。对于所有安全密级\(l_i ,i=0,…,k-1\),有\(l_i < l_{i+1}\)。
简单安全属性:
S可以读0,当且仅当\(l_o < l_s\), 且s对o具有自主型读权限。
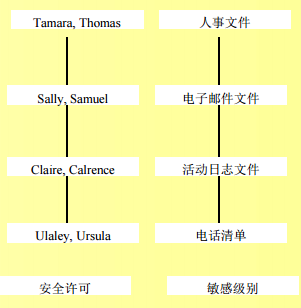
例如:例如,在上图中,Claire和Clarence不能读人事文件,但Tamara和Sally可以读活动日志文件(而且,实际上根据Tamara的安全许可,她可以读任何文件在此假设自主型访问控制允许Tamara和Sally的访问 )。
*-安全属性
s可以写o,当且仅当\(l_s < l_o\)。且s对o具有自主型写权限。
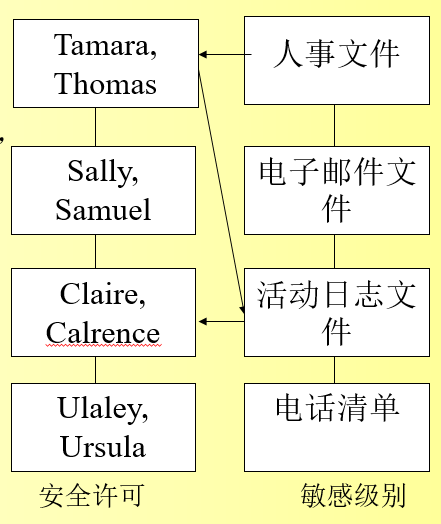
例如:如果Tamara(Top Secret )决定将人事文件的内容复制到活动日志文件里,并设置适当的自主访问权限,那么Claire(Confidential )就可以读这些人事文件了。这样,Claire可能会读取到具有更高安全等*-属性级的文件。
这时因为活动日志文件的安全密级为C,Tamara的安全许可为TS,所以她不能写活动日志文件。
类别
通过给每个安全密级增加一套类别,每种类别都描述一种信息,可以将模型进行扩展。属于多个类别的客体拥有所有属于这些类别的信息。
这些类别来自于“需要知道’’原则,它规定,除非主体为了完成某些功能而需要读取客体,否则就不能读取这些客体。某人可以访问的类别集合就是类别集合的幂集。
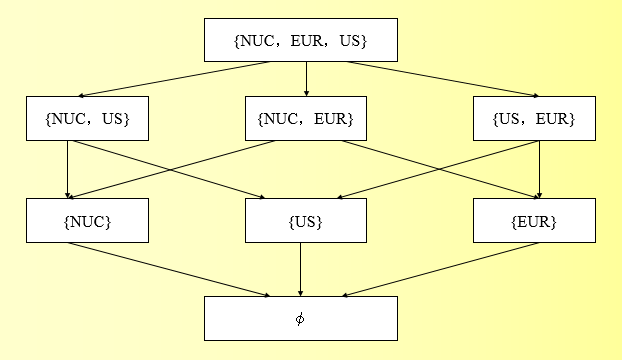
例如,如果类别是NUC,EUR和US,那么某人可以访问的类别集合就是以下集合之一:
\[ φ(空集),\{NUC\},\{EUR\},\{US\},\{NUC,EUR\} , \{EUR,US\} , \{NUC,US\} , \{NUC,EUR,US\} \]
这些类别集合在操作⊆(子集关系)下形成一个格。子集之间具有偏序关系:
安全等级
-
每个安全级别和类别形成一个安全等级。
安全等级 = < 安全级别, 类别 >
-
主体的安全等级表示了主体的安全许可等级。
-
客体的安全等级表示了客体的敏感性,所需的保护等级。
例如: \(George的安全等级=(TOP SECRET, \{NUC,US\} )\)。William的安全等级=\((SECRET,\{EUR\})\)文档f.docx的安全等级=\((CONFIDENTIAL,\{US\} )\)。
类别基于“需要知道”原则,所以预先假设对类别集合\(\{EUR\}\)有访问权的人没有必要访问类别\(\{NUC,US\}\)里元素。因此,即便该主体的安全许可高于客体的安全密级,读访问也应该被拒绝。
支配关系
支配(dominates)关系:表示安全级别和类别集合之间的结合关系。
定义: 安全等级\((L, C)\)与\(( L’ , C’)\)满足\(L’ ≤L\),\(C’ ⊆ C\),则称\((L, C)\)支配\(( L’ , C’)\),记为: \[ ( L’ , C’) ≺ (L, C) 或者 (L, C) dom ( L’ , C’) \]
支配关系\(≺\)为安全等级集合上引入了一个格。
基本安全定理
设系统\(∑\)的某一个初始安全状态为\(σ_0\),\(T\)是状态转换的集合。如果\(T\)的每个元素都遵守简单安全条件和*-属性,那么对于每个\(i ≥ 0\),状态\(σ_i\)都是安全的。
形式化描述
- 模型的元素
| 集合 | 元素 | 语义 |
|---|---|---|
| S | \(\{S_1,S_2, .... ,S_n\}\) | 主体: 进程 |
| O | \(\{O_1,O_2, .... ,O_m\}\) | 客体:数据、文件、程序、设备等。 |
| C | \(\{C_1,C_2, ....,C_q\} C_1 > C_2 > .... > C_q\) 级别:主体的安全许可,客体的敏感级别。 | |
| K | \(\{K_1,K_2, ....,K_r\}\) | 类别:访问权限范围。 |
| A | \(\{r,w,e,a,c\}\) | 访问属性:read, write, append, execute, control |
| RA | \(\{g,r,c,d\}\) | 请求元素: g: get, give r: release, rescind c: change, create d: delete |
| R | \(S^+ × RA × S^+ × O × X 其中: S^+ = S ∪ \{f\}, X = A ∪ \{f\} ∪ F; 一个请求的元素记为 R_k\) | 请求:inputs, commands, requests for access to objects by subjects |
| D | \(\{yes, no, error, ?\}D的元素记为D_m\) | 决定 |
| F | \(C^S × C^O × (PK)^S × (PK)^O\) an arbitrary element of F is written \(f = (f_1,f_2,f_3,f_4)\) | classification/need-to-know vectors; f1: subject-classification function f2: object-classification function f3: subject-category function f4: object-category function |
| X | \(R^T\) an arbitrary element of X is written x. | request sequences |
| Y | \(D^T\) an arbitrary element of Y is written y. | decision sequences |
| M | \(\{M_1,M_2, .... , M_c\}, c = {(2^5)}^{n·m}\); an element of M, say M_k, is an n × m matrix with entries from PA; the \((i,j)‑entry\) of \(M_k\)shows \(S_i\)’s access attributes relative to \(0_j\) | access matrices |
| V | \(P(S × O × A) × M × F\) an arbitrary element of V is written v. | states |
| \(Z=V^T\) | \(T = \{1,2,…, n\}, V_T=\{(v_1, …, v_n ) | ∀i∈T, v_i∈V \}\), An arbitrary element of \(V_T\) is written z, which is a state sequence ; The components of a state sequence z are\(v_t\), \(t=1,2,…, n\), and they are also denoted as \(z_t\) ,which is the t-th state in the state sequence, \(t=1,2,…, n\)。 | state sequences |
BINISM
/
/ - views
Published under(CC) BY-NC-SA 3.0 CN.