取予（Take-Grant）保护模型

Posted by BINISM on June 23, 2016

目录

取予模型定义

取予（take-Grant）保护模型是访问控制矩阵模型中的一种，使用有向图的形式来表示系统，称这样的有向图为保护图。

节点 可以是主体或客体。节点可能是主体或客体的。

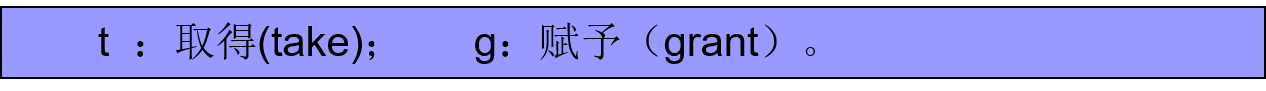取予模型节点 边都标记为从源点到目标节点的权限。权限就是预定义的集合R，R含有两个特殊权限 取予模型特殊边的定义 Take规则： 设x，y和z是保护图G0的三个不同节点，并且x是一个主体。设x到z有一条标记为 \(\gamma\) 的边，且 \(t\in\gamma\) ,z到y有一条边 \(\beta\) 且 \(\alpha\subseteq\beta\) 。Take规则定义了一个新图G1，新图在原有的保护图上加入了一条x到y的标记为 \(\alpha\) 的边。从图上看，这条规则被写为“x从y中取得了到y的权限 \(\alpha\) ”。

Take G0

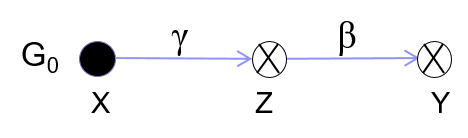
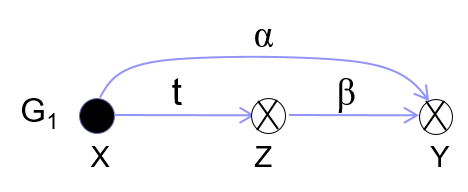
Take G1

表示成G0├─ G1 ：“x从y中取得了到y的权限 \(\alpha\) ”

Grant规则: 设x，y和z是保护图G0的三个不同节点，并且z是一个主体。设z到x有一条标记为 \(\gamma\) 的边，且 \(g\in\gamma\) ，z到y有一条边 \(\beta\) ，且 \(\alpha\subseteq\beta\) 。Grant规则定义了一个新图G1，新图在原有的保护图中加入了一条x到y的标记为 \(\alpha\) 的边。从图上看这条规则别写为“z赋予了x到y的权限 \(\alpha\) ”。

Grant G0

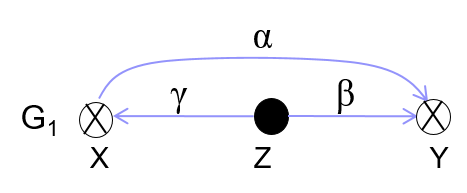
Grant G1

表示成G0├─ G1：├─“z赋予了x到y的权限 \(\alpha\) ”。

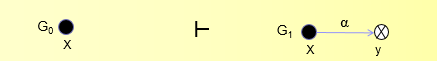
Create规则： 设x是保护图G0的一个主体，并且 \(\alpha\subset R\) 。Create规则定义了一个产生新图的G1方法（1）加入一个新的节点y;(2)加入一条从x到y的标记为 \(\alpha\) 的边。这条规则称为：“x通过权限 \(\alpha\) 创建了节点y。” Create

Remove规则： Remove规则：设x、y是保护图G0的两个节点，并且x是主体。从x到y存在一条标记为β的边，并且 \(\alpha\subseteq\beta\) 。Remove规则定义了一个产生新图的G1方法：新图中边的标记 \(\beta\) 变为 \(β-α\) ，如果结果为空集，则边要被去掉。

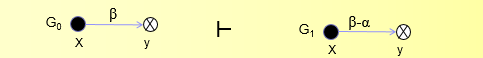
Remove

权限共享

定义: 设G0是一个保护图，x,y是\(G_0\)中两个不同实体节点， \(\alpha\) 是权限集合\(R\)的一个子集。谓词\(can·share(\alpha,x,y，G_0)\)的意义是：

  1. 存在一个保护图的序列\(G_1, G_2, ……,G_n， ρ_i,i=1,……，n\), 利用规则\(ρ_i\)可以实现\(G_{i-1} ⊢ * G_i, i=1,……，n\)；
  2. Gn中存在包含权限子集 \(\alpha\) 的x到y的边；

引理：

引理

证明：

x创建了新节点v，并且边标记为tg。

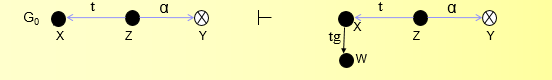
证明step1

z从x取得了到v的权限g。

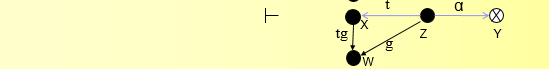
证明step2

z赋予了v到y的权限 \(\alpha\) 。

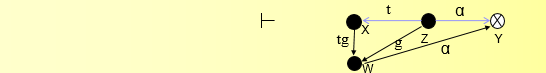
证明step3

x从v中取得了到y的权限 \(\alpha\) 。

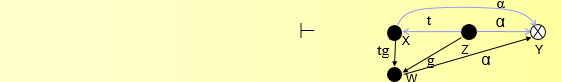
证明step4

类似的证明可得出以下引理：

引理：

引理

主体对称性

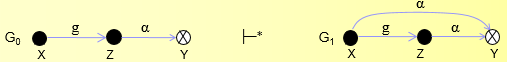
主体对称性

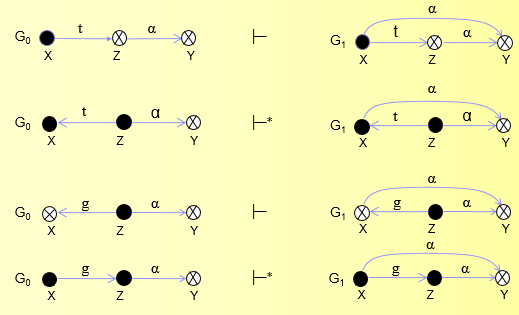
对称性： 如果连接x和y的tg路径中的节点都是主体，则Take和Grant规则是对称的。

定义： 一个岛屿是最大的tg相连的、仅有主体的子图。

共享： 一个岛屿是仅有tg相连的最大子图。

可以直接证明任何节点所拥有的任何权限都可以被岛屿中的其他节点所共享。

岛屿之间的权限转移：

  • 一个岛屿中的一个主体可以从另一个岛屿中的节点取得权限；
  • 一个主体可以赋予权限给一个中间主体，而另一个岛屿中的某个主体可以从该主体中取走这个权限。

定义： 桥是指二个连接端点主体v0和vn的tg路径，并且与该路径相关联的字串在集合\(\{ \overset{\to}{t}* , \overset{\to}{t}* \overset{\to}{g} \overset{\gets}{t}* ,\overset{\to}{t}* \overset{\gets}{g} \overset{\gets}{t}* \}\)中。

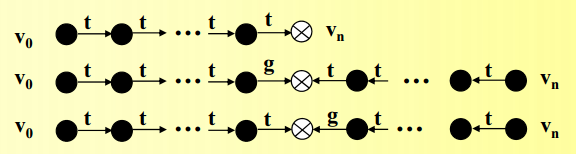
桥的端点都是主体，所以权限可以从桥的一端转移到另一端。

共享模型

定理： 谓词\(can·share(\alpha,x,y，G_0)\)的意义是：

  1. x,y是主体并且存在一条由x到y的边标记为α；或者
  2. 如下条件同时成立:
    • G0中存在主体s，且存在s到y的标记为α的边;
    • 存在岛屿\(I_1,I_2,…，I_n\)，x在\(I_1\)中，s在\(I_n　\)中，并且\(I_j\)到\(I_{j+1}(1≤j<n)\)都存在一座桥。

当桥的两端是客体时，就不再具有对称性，共享定理不再成立。

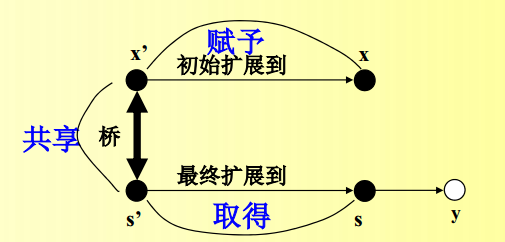
定义： 如果x是一个主体，并且在x, y之间存在一条tg路径具有关联字串定义在集\(\{ \overset{\to}{t} * \overset{\to}{g} \} \cup \{v\}\) 中，则节点x可以初始扩展到y。其中v表示空串。

定义： 如果x是一个主体，并且在x, y之间存在一条tg路径具有关联字串定义在集\(\{ \overset{\to}{t} * \} \cup \{v\}\) 中，则节点x可以最终扩展到y。其中v表示空串。

如果y是客体，则x无法获得y拥有的权限。——不对称性！

定理： 谓词\(can·share(\alpha,x,y，G0)\)为真的充要条件是：

  1. 存在一条由x到y的标记为α的边；或者
  2. 如下条件同时成立:
    • G0中存在节点s，且存在s到y的标记为α的边;
    • 存在一个主体节点x’，且x’=x 或者x’初始扩展到x;
    • 存在一个主体节点s’，且s’=s 或者s’最终扩展到s;
    • 存在岛屿\(I_1,I_2,…，I_n\)，且x’在\(I_1\)中，s’在\(I_n\)中，并且\(I_j\)到\(I_{j+1}(1≤j<n)\)都存在一座桥。

偷窃模型(steal mode)

定义： 设G0是一个保护图，x,y是G0中两个不同实体节点，α是权限集合R的一个子集。谓\(can·steal(α,x,y)\)的意义是：

  1. 不存在包含权限子集α的x到y的边；
  2. 存在一个保护图的序列\(G_1, G_2, ……,G_n\)使得以下条件同时成立：
    • \(G_n\)中存在包含权限子集α的x到y的边;
    • 存在一个状态转换规则序列：\(ρ_i,i=1,……，n\), 使得利用规则\(ρ_i\)实现 \(G_{i-1} ├ G_i, i=1,……，n\)。
    • 对于Gi-1中的任意节点v和w，1≤i<n，如果在G0中存在v到y的包含权限α的边，则不是“v将对于y的权限α授予w”形式的规则。

注：这个条件是要求任何对y拥有α权限的节点不能将这个权限授予其它节点.

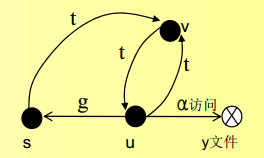
例如： 一个教授拥有学生的成绩单文件，他不会对这个文件的访问权限授予任何其它的主体。 问题是：这个系统中的其它主体可以通过系统的规则获得（窃取）这个文件的访问权限吗？

  • u不希望将对y的权限α授予他人;
  • u 将其它的权限(对v的t权限)授予s;
  • 这时s可以从v取得对u的t权限；
  • 这样s就可以取得u的对w的α权限了。

访问控制抽象

  1. 权能模式
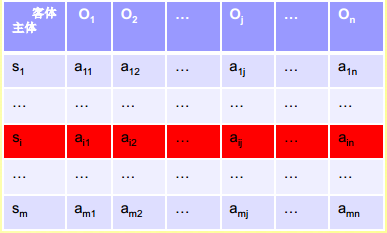
    • 对应访问控制矩阵中的行结构。
    • 面向门票的模式，以主体为中心，阐述每个主体能够访问的所有客体及其访问的方式。
    • 例：现代的属性证书
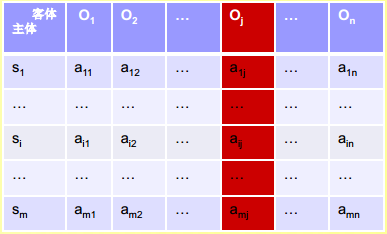
  2. 访问控制表模式
    • 与访问控制矩阵中的列结构相对应。
    • 以客体为中心，确定能够访问该客体的所有主体的名单集合。
    • 例：Windows 的NTFS的权限管理方式。

安全性

  1. 访问控制矩阵只是表达了主体与客体的权限关系，这样的关系是否满足管理者的要求？如何进行控制能够继续保持满足管理者的要求？
  2. 是否存在一个谓词来表达系统的“安全状态”？
    • 安全性需要进行抽象，怎样表达安全目标。
  3. 在给定的安全状态下，什么样的行为规则可以保障系统可以保持处于安全状态？
    • 需要研究行为与保护状态的转换的关系，如何对行为进行控制。

BINISM / /  -  views
Published under(CC) BY-NC-SA 3.0 CN.

友情链接